Knowledge Distillation and Incremental Learning

A detailed introduction to Knowledge distillation from complex neural networks and a much needed end to end Incremental Learning technique.

A Catastrophe

Imagine training an object detection model on an extensive amount of data, with well-defined label and bounding box annotations. State of the art detectors perform quite well and clever tweaks like the Focal Loss mechanism have led to the development of single-stage detectors with comparable or even better accuracy. However, even with the most extensive of datasets, a problem still persists, and is quite catastrophic in nature.

The problem is called catastrophic forgetting and stems from the fact that the model trained on a given dataset is only able to classify amongst a finite set of objects. When new classes are added, one might be tempted to train the existing model on these samples and expect the model to not only correctly detect objects of the new category, but also the objects from the older category. However, the model’s performance when it comes to the older classes, diminishes dramatically. A workaround for this problem is to train the model on the entire collection of data, both old and new. The troubles associated with this approach is quite evident. Even if this can be done for one or two new classes, it becomes unsustainable for incrementally growing number of classes. Put simply, traditional Deep Learning models need to have all the data available to them while training. They are not equipped to selectively learn about new data with a small collection of the data.

The Paper discussed here is titled “End-to-End Incremental Learning” and discusses an approach to learn deep neural networks incrementally, using new data and only a small exemplar set corresponding to samples from the old classes. The end-to-end learning objective comprises of two parts: A distillation based measure to retain knowledge from old classes, and a usual cross entropy based measure to learn new classes. The approach discussed here is Incremental as, it has the ability to train itself from a flow of data and performs decently well, while classifying both old and new classes. It is also an end to end system where the classifier and feature representation is updated in a joint fashion. Essentially, this method can be plugged into any deep learning architecture by replacing the traditional loss function with a cross distilled loss function.

Distillation - It’s a thing

Before we move ahead to discuss more about the cross-distilled loss, we might as well discuss a bit about the Distillation technique proposed here in this paper titled “Distilling the Knowledge in a Neural Network”. Now, this paper is really interesting in its own right, and no surprised there, having been written jointly by Hinton, Vinyals and Jeff Dean. The entire objective of the paper is to present an approach where one can train a highly complex model on a large amount of data and empower the model to extract structure from the data. Following this training, the authors have shown a way to transfer this knowledge to a small model that is more suitable for deployment and has less rigid requirements in terms of latency or performance.

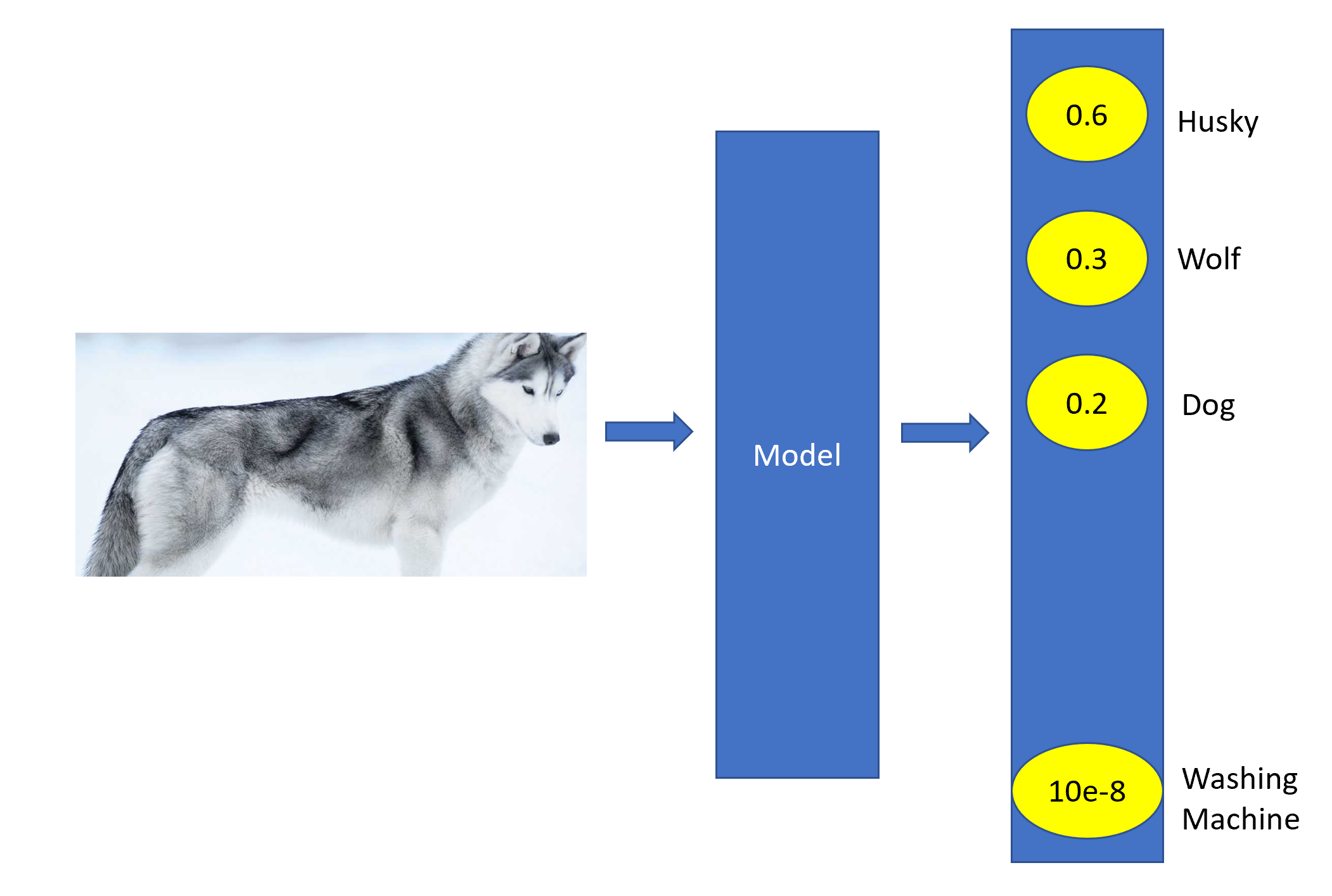
When an image is passed to an Image Classification network, we identify the knowledge learnt in the model by checking the log probability of the correct answer. For instance in the figure below, the model is able to classify the image correctly, as the probability is highest for the category Husky. However, the question at hand is: How do we change the form of the model but keep the same knowledge?. By training the model on the objective of maximizing ground truth log probability, a beneficiary side effect that we can observe is that the model assigns probabilities to all incorrect answers as well. Even though these probabilities are really small, some of them are much larger than the others. For instance, the categories Wolf and Dog have much higher probability than say, Washing Machine. Quoting from the paper itself:

These relative probabilities of incorrect answers tell us a lot about how the cumbersome model tends to generalize.

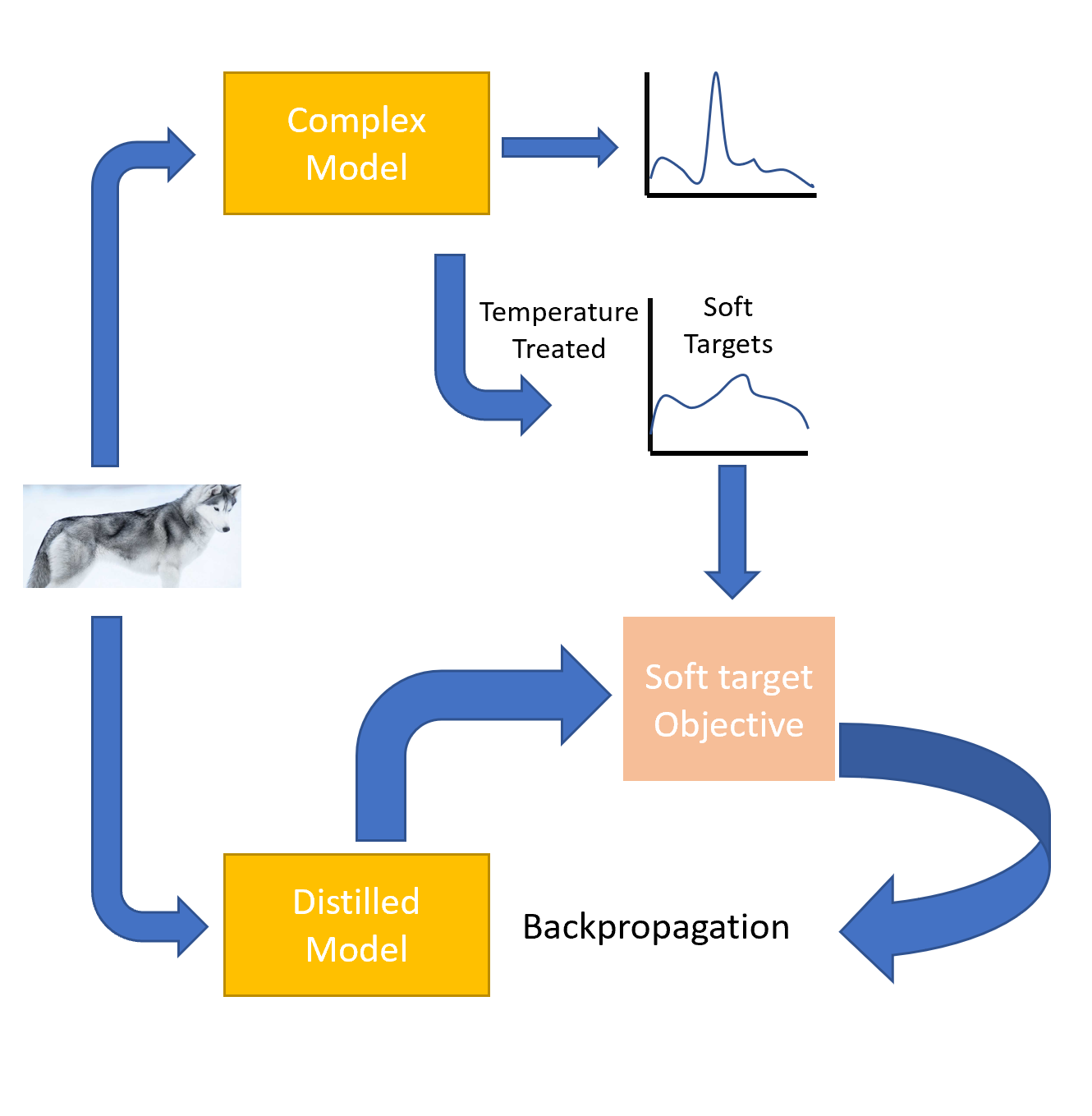
This generalization ability is the key idea behind the idea of distilling knowledge appropriately from a much bigger model into a smaller model. If a small model is trained on the same dataset as a much more complex model and its performance is compared to another smaller model which is derived by distilling the knowledge from a complex model trained on the same dataset, we can see that the latter model performs better. This generalization ability is transferred to small models by using the class probabilities produced by the cumbersome model as “soft targets”. A separate transfer set or the same training set can be used. If the soft targets tend to follow a uniform distribution, or in other words, have more entropy, they tend to convey more information about the image than the hard target alone. Moreover, this also provides less variance in gradient between training cases, leading to the requirement of much less training data for the small model. Previous methods have used the logits produced by complex models directly to extract information from the soft targets. However, a much more meaningful way to do so is the distillation technique in which one raises the temperature of the softmax produced by the complex model.

Raising the Temperature

A softmax converts the logit computed for each class into a probability by comparing the corresponding logit to all other logits.

\[ q_i = \frac{\exp{(z_i / T)}}{\sum_{j} \exp{(z_j / T)}}\]

In the above formulation, we are introduced to this Temperature parameter \(T\). Normally, it is set to 1. A higher value of T generates a softer probability distribution over classes. The steps involved in the simplest form of distillation are:

• Train a distilled model by training it on a transfer set
• Training is done using a soft target distribution for each case in the transfer set by using the complex model
• The complex model uses the same temperature in its softmax
• The same temperature is also used when training the distilled model
• Post training, the temperature is lowered to 1.

An additional step that can be added is to introduce a loss function that checks if the distilled model can match the correct output label of the image. This is possible only when the transfer set has correctly labeled images. In such a case, one can use a weighted average of the two objective functions. The first objective function is the cross entropy with the soft targets and this is computed using the same high temperature as in the softmax for the complex model. For the first objective, we have a cross entropy with the correct labels. The latter is usually weighed less.

End to End Incremental Learning

This section is dedicated to the study of incremental learning in an end-to-end approach, designed using a deep learning architecture. This method uses a representative memory component that is similar to maintaing a small set of samples corresponding to old, learned classes. Think of this as the notes you keep in class about the stuff you understood. You remember most of it, but you still need to refer it to keep yourself updated. This method uses a deep network trained on a cross distille loss function. A typical descriptive figure provided in the paper is as follows:

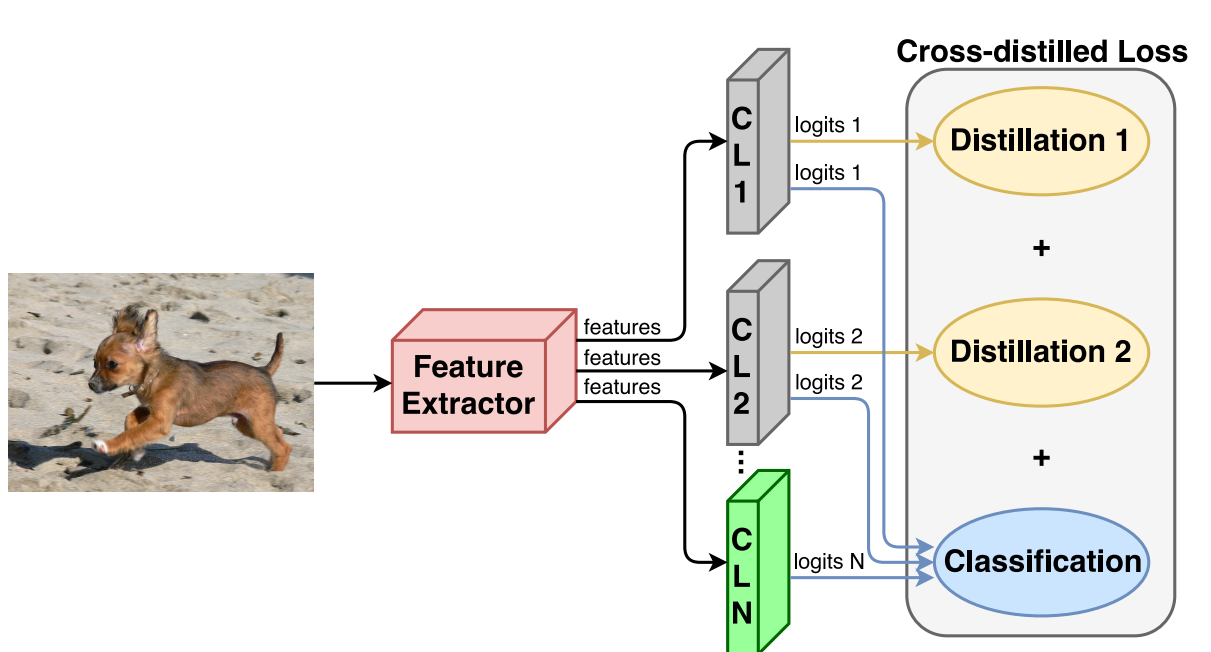
This model has one classification layer and a classification loss. This layer uses features from the feature extractor to produce a set of logits. These logits are transformed into clas scores by a softmax layer. To help the model retain knowledge from the old classes, this method uses a representative memory unit. Let’s discuss this representative memory unit in further detail.

Representative Memory

The objective of this unit is to create a subset with the most representative samples from a class and to store them separately in a memory space. One can limit the memory capacity to \(K\) samples, leading to \(\frac{K}{n}\) samples for each of the \(n\) classes. One can also fix the number of samples for each class at c, leading to a memory of size \(cn\). The functionality of this memory is two fold.

• Selection of new samples: To choose the most representative elements of a class, we can select the ones closest to the mean sample of that class.
• Removing samples: This operation is performed after the training process to allocate memory for the samples from the new class.

Network Architecture

In this section, we discuss the network architecture in greater detail. As seen in the figure, the network has several components. One of them is the feature extractir which corresponds to a set of layers that transforms the input image into a feature vector. The classification layer takes these features and produces a set of logits. The general procedural flow is as follows:

• Begin with traditional non-incremental architecture for classification.
• When new classes are trained, add a new classification layer and connect it to feature extractor layer
• Any pre-trained architecture can be used as feature extractor layer

Cross Distilled loss function

This loss function has two main parts: A Distillation loss \(L_{D_f}\), and a Multi-class cross entropy loss \(L_C\).

\[L(\theta) = L_C(\theta) + \sum_{f=1}^{F}L_{D_f}(\theta)\]

It is to be noted that the distillation loss is applied only on the old classification layers, whereas the cross entropy loss is applied on samples from old and new classes. The distillation loss ensures that the model doesn’t suffer catastrophic failure by improving the generalization ability of the classifier on the older classes. The cross entropy loss enhances the overall discriminative power of the classifier.

Incremental Learning Procedure

The Incremental Learning step has four main steps as illustrated in the following figure:

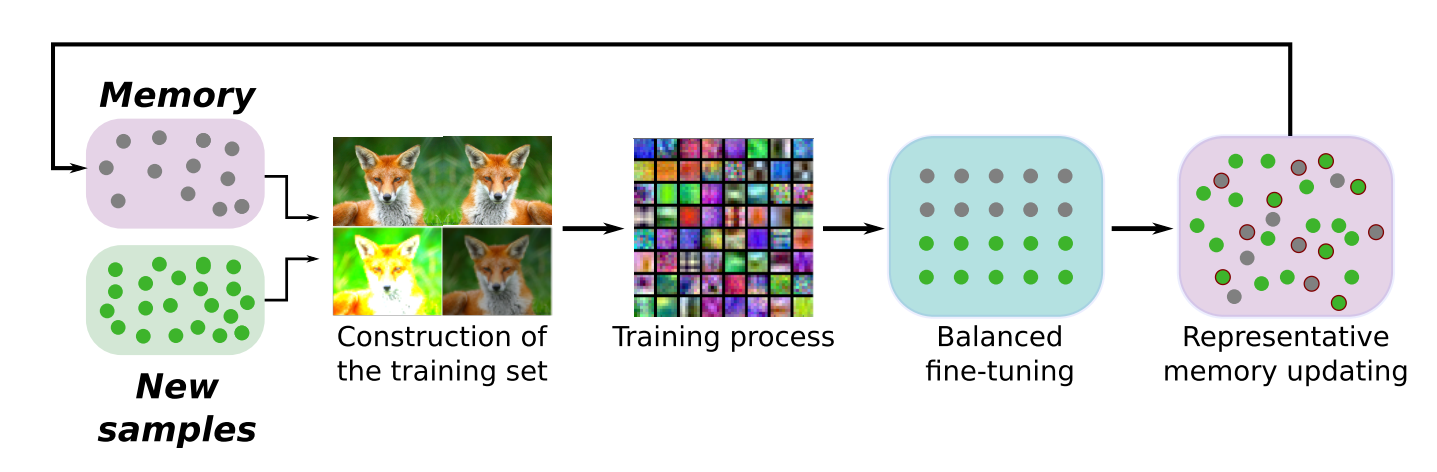
• Construction of the Training set: The training set should have samples from both new and old classes. The design of the loss function is such that each sample should have two associated labels. For the classification loss component \(L_C\), we use the one-hot encoded vector. For the distillation loss component \(L_{D_f}\), we use the logits produced by every classification layer with old classes. Each image in the training set has a classification label and \(F\) distillation labels, where \(F\) is the number of old classification layers.
• Training: During training, all weights are updated. For any sample, the features obtained from the feature extractor are likely to change between successive incremental steps. The classification layer should adapt to this.
• Balanced Fine Tuning: To deal with the unbalanced training scenario with regard to new and old classes, the authors introduce an additional fine-tuning stage with a small learning rate and a balanced set of samples. This subset has samples from all classes, old and new. To prevent the model from forgetting the knowledge it acquired in the previous step, the authors added a temporary distillation loss to the classification layer of the new class.
• Representative Memory Update: The representative memory must be updated to include exemplars from the new class. The selection and removal operations are conducted in a fashion as discussed previously.

Training Procedure

Since a readily available setup is not available to tes incremental learning benchmarks, the authors split the classes of traditional multi-class dataset into incremental batches. Standard data augmentation steps are also included before any kind of training in the network. The datasets used are CIFAR-100 and ImageNet. The number of classes in each incremental step has also been changed during experimentation, as seen in the following figure. The results for CIFAR-100 are promising. In the left graph, one can see the classes being increased by 2 in each incremental step, whereas on the right, the classes are being increased by 5 in each incremental step.

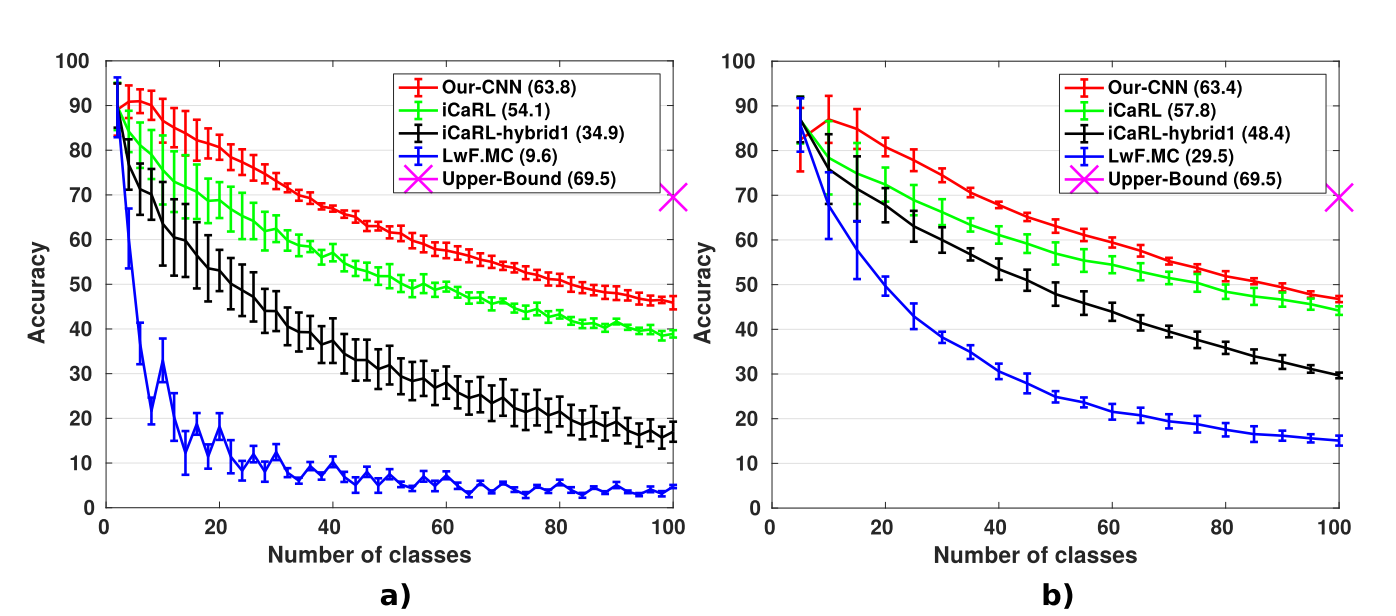
For ImageNet, there is a marked difference in the performance of the model when the number of classes is changed from 10(on the left) to 100(on the right), as seen in the following figure.

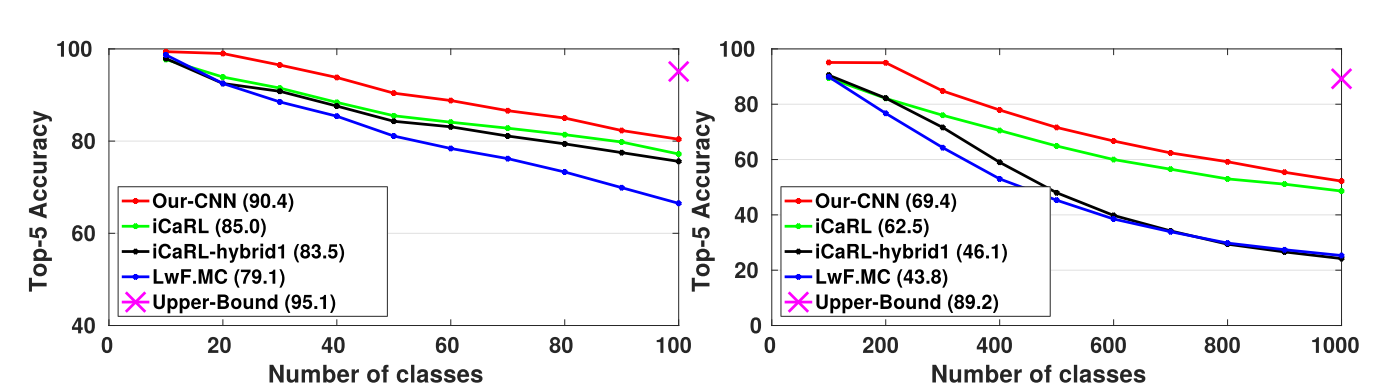
This method performs consistently well on both the datasets and outperforms other state of the art results. The following tables represent the incremental approach with the number of classes in each step denoted as columns. The left table shows results for the CIFAR-100 dataset, whereas the right table shows results for the ImageNet dataset.

To conclude, this post is intended to help get a better understanding of Knowledge Distillation from complex networks to smaller networks. This enables the transfer of knowledge from much more complex networks to simpler networks. This is done by using the distillation technique that transfers the generalization ability of the complex network to the simpler network, instead of transferring the exact discriminative ability of the complex network. This idea is used to develop an incremental approach. This model trains end to end and based on experimentation, performs better than other state of the art results.

Thanks for reading!